ECUACIÓN EXPLICITA DE LA RECTA
Si en la ecuación general de la recta:
despejamos y, se obtiene la ecuación explícita de la recta:
El coeficiente de la x es la pendiente, m.
El término independiente, b, se llama ordenada en el origen de una recta, siendo (O, b) el punto de corte con el eje OY
Ejemplos:
Hallar la ecuación en forma explícita de la recta que pasa por A (1,5) y tiene como pendiente m=-2.
1. Halla la ecuación de las siguientes rectas:
- a) Tiene pendiente -2 y ordenada en el origen 3.
- b) Tiene pendiente 4 y pasa por el punto
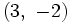 .
. - c) Pasa por los puntos
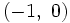 y
y 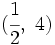 .
. - d) Pasa por el punto
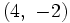 y es paralela a la recta
y es paralela a la recta 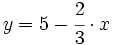 .
.
Sean
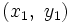
y
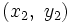
dos puntos de una recta (
que no sea horizontal *), entonces la ecuación de la recta viene dada por la expresión:
expresión que se denomina ecuación continua de la recta.
Además, su pendiente es:
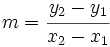
.
(* La recta no puede ser horizontal porque si no el primer denominador se anula)





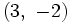 .
.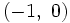 y
y 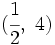 .
.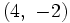 y es paralela a la recta
y es paralela a la recta 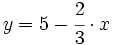 .
.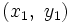 y
y 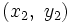 dos puntos de una recta (que no sea horizontal *), entonces la ecuación de la recta viene dada por la expresión:
dos puntos de una recta (que no sea horizontal *), entonces la ecuación de la recta viene dada por la expresión: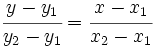
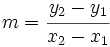 .
.
No hay comentarios.:
Publicar un comentario