FUNCIÓN CUADRATICA

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida por:
con  .1
.1
 .1
.1
Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").
El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.
Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales 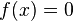 . Son denotadas habitualmente como:
. Son denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.
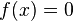 . Son denotadas habitualmente como:
. Son denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.- Dos soluciones reales y diferentes si el discriminante es positivo:
-
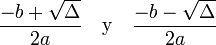 .
.
- Corta la parábola al eje X en dos puntos diferentes.
- Una solución real(o solución doble) si el discriminante es cero:
- La parábola es tangente al eje X.
- La parábola no corta al eje X.
- El único caso restante es que el discriminante sea negativo. En tal caso, las raíces no son reales, sino que son dos números complejosconjugados:

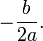
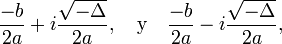
No hay comentarios.:
Publicar un comentario